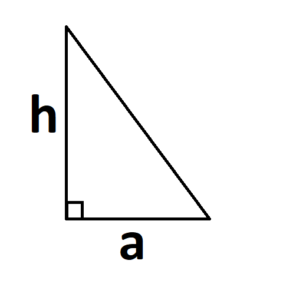Путеводитель по геометрическим фигурам и формулам
Геометрия – одно из важнейших разделов математики, изучающий пространственные фигуры и их свойства. Знать геометрию необходимо при решении многих задач в различных областях жизни, начиная от архитектуры и окончая дизайном. В этом путеводителе мы рассмотрим основные геометрические фигуры и формулы для их вычисления.
Линии
Прямая
Прямая – это геометрическая фигура без начала и конца, которая простирается в бесконечность в обе стороны. Прямая характеризуется коэффициентом наклона и углом наклона.
Формула угла наклона:
$\alpha=\arctan{\dfrac{k}{1}}$
где $k$ — коэффициент наклона.
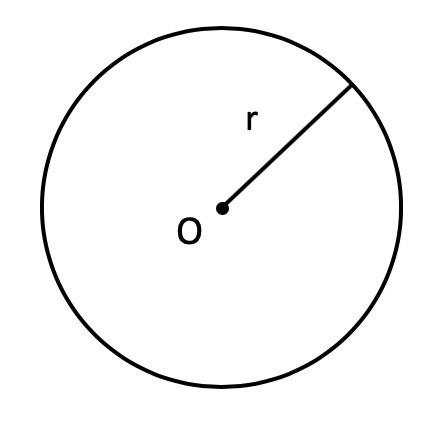
Окружность
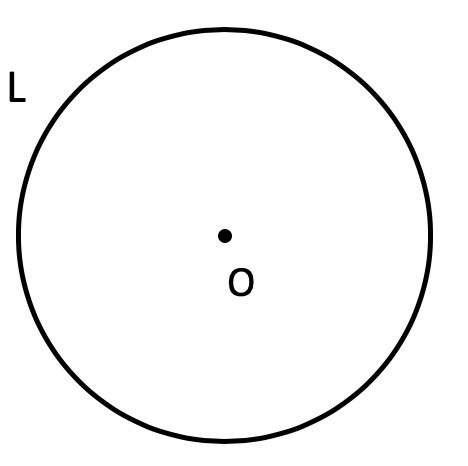
Окружность – это геометрическая фигура, которая состоит из всех точек плоскости, находящихся на одном и том же расстоянии от центра.
Формулы для вычисления площади ($S$) и длины ($L$) окружности:
$S=\pi r^2$
$L=2\pi r$
где $r$ – радиус окружности.
Плоские фигуры
Квадрат
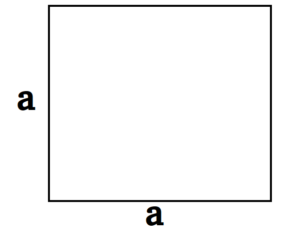
Квадрат – это плоская геометрическая фигура, имеющая четыре равные стороны и углы в 90 градусов.
Формулы для вычисления площади ($S$) и периметра ($P$) квадрата:
$S=a^2$
$P=4a$
где $a$ – длина стороны квадрата.
Прямоугольник
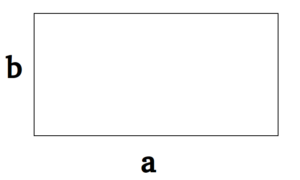
Прямоугольник – это плоская геометрическая фигура, у которой противоположные стороны равны и все углы прямые.
Формулы для вычисления площади ($S$) и периметра ($P$) прямоугольника:
$S=a\cdot b$
$P=2a+2b$
где $a$ и $b$ — длины сторон прямоугольника.
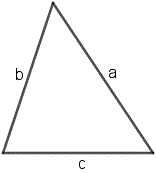
Треугольник
Треугольник – это плоская геометрическая фигура, имеющая три стороны, три угла и три вершины.
Формула для вычисления площади ($S$) треугольника по формуле Герона:
$S=\sqrt{p(p-a)(p-b)(p-c)}$
где $p=\dfrac{a+b+c}{2}$ — полупериметр треугольника, $a$, $b$, $c$ — длины сторон треугольника.
Пространственные фигуры
Куб
Куб – это пространственная фигура, имеющая шесть граней, каждая из которых является квадратом.
Формулы для вычисления объема ($V$) и площади поверхности ($S$) куба:
$V=a^3$
$S=6a^2$
где $a$ – длина стороны куба.
Цилиндр
Цилиндр – это пространственная фигура, которая состоит из двух круглых оснований и боковой поверхности, образованной прямоугольником, который проходит через центры оснований.
Формулы для вычисления объема ($V$) и площади поверхности ($S$) цилиндра:
$V=\pi r^2h$
$S=2\pi r^2+2\pi rh$
где $r$ – радиус основания, $h$ – высота цилиндра.
Шар
Шар – это пространственная фигура, которая состоит из всех точек пространства, находящихся на одном и том же расстоянии от центра.
Формулы для вычисления объема ($V$) и площади поверхности ($S$) шара:
$V=\dfrac{4}{3}\pi r^3$
$S=4\pi r^2$
где $r$ – радиус шара.
Заключение
В этом путеводителе мы рассмотрели основные геометрические фигуры и формулы для их вычисления. Зная эти простые правила, можно решить многие задачи, связанные с геометрией.
Geometric shapes are the figures used in mathematics to represent the forms of real-world things. Shapes are the forms of things in geometry that have boundaries, angles, and surfaces.
There are basically two types of geometric figures:
- 2D Shapes(Two-dimensional)
- 3D Shapes(Three-dimensional)
Shapes are also divided into two types on the basis of their regularity or uniformity.
- Regular Shapes– Symmetric shapes such as square, circles, etc.
- Irregular Shapes– Asymmetric shapes or freeform shapes.
Types and Properties of Geometric Shapes
2D Shapes
| Name | Figure | Definition |
|---|---|---|
| Square |
|
A square is a 2D figure consisting of 4 equal sides and equal angles, where each angle is equal to 90°. |
| Rectangle |
|
A rectangle is a 2D figure with 4 sides where opposite sides are equal and each angle is equal to 90°. |
| Triangle |
|
A triangle is a 2D figure enclosed with 3 sides and consists of 3 edges and 3 vertices and has the sum of its 3 angles equal to 180. |
| Circle |
|
A circle is a closed 2D figure round in shape with no sides and corners. |
| Oval |
|
An oval is also a closed 2D figure somewhat similar to a circle with elongated to some extent. It does not have |
| Parallelogram |
|
A parallelogram is a quadrilateral with two pairs of parallel sides and equal opposite angles. |
| Trapezium |
|
A Trapezium is a quadrilateral in which one pair of opposite sides is parallel. |
| Rhombus |
|
Rhombus is a type of quadrilateral.It is a special parallelogram that has 4 equal sides and its diagonals bisect at 90. |
| Kite |
|
Kite is a quadrilateral that has two pairs of equal adjacent sides. |
Types of Polygons
| Shapes | Figures |
|---|---|
| Triangle |
|
| Quadrilateral |
|
| Pentagon |
|
| Hexagon |
|
| Septagon |
|
| Octagon |
|
| Nonagon |
|
| Decagon |
|
3D Shapes
| Names of 3D geometric shapes | Figure | Definition |
|---|---|---|
| Cube |
|
A cube is a three-dimensional shape that has 6 faces, 8 vertices, and 12 edges. The faces of the cube are square. Example: A Rubik’s cube |
| Cuboid |
|
A cuboid is a three-dimensional solid having 6 rectangular faces, 8 vertices, and 12 edges. Example: Matchbox |
| Cone |
|
A cone is a solid which has a circular base and a pointed edge at the top called the apex or vertex. Example: An ice cream cone |
| Cylinder |
|
A cylinder is a 3d solid shape that has two parallel circular bases connected by a curved surface. It has no vertex. Example: Gas cylinder |
| Sphere |
|
A sphere is a round shape in a 3d plane, looking like a ball. Its radius extends in three dimensions (x-axis, y-axis, z-axis). Example: Ball |
List and Properties of Geometric Shapes
The list of geometric shapes along with their edges, vertices, and faces is given below.
| Name | Type | Edges | Vertices | Faces |
|---|---|---|---|---|
| Square | 2D | 4 | 4 | — |
| Rectangle | 2D | 4 | 4 | — |
| Triangle | 2D | 3 | 3 | — |
| Circle | 2D | Curved | 0 | — |
| Pentagon | 2D | 5 | 5 | — |
| Hexagon | 2D | 6 | 6 | — |
| Cube | 3D | 12 | 8 | 6 |
| Cuboid | 3D | 12 | 8 | 6 |
| Cone | 3D | 1 | 1 | 2 |
| Cylinder | 3D | 2 | 0 | 3 |
| Sphere | 3D | Curved | 0 | 1 |
Open and Closed Figures
Closed Shapes
Basic geometric shapes like squares, rectangles, and triangles are a few 2D shapes. These figures are referred such as polygons. Any flat form or plane on a piece of paper is a polygon. They have finite closed boundaries made up of line segments known as sides of the polygon. Geometric figures such as polygons are known as closed figures. The boundary of a closed figure could be either made up of line segments or curves. Therefore, any geometric object that begins and ends at the same location and forms a border using line segments or curves is considered to be a closed figure.
Open Shapes
Open shapes aren’t complete. The beginning point and finishing point must be met in order to draw a closed figure. Using line segments or curves to represent open figures is another option, but at least the lines will be broken up. The origin and destination of an open figure are distinct.
FAQs on Geometric Shapes
Q1: What are different geometric shapes in Maths?
Answer:
There are various geometric shapes such as circle, square, rectangle, kite, triangle etc. are the basic 2d shapes while Cube,Cuboid,Cone,Cylinder,Sphere are basic 3d shapes.
Q2: Name different kinds of polygons.
Answer:
The different polygons are:
Triangle
Quadrilaterals – square, rectangle, parallelogram, trapezium, kite
Pentagon
Hexagon
Heptagon
Octagon
Nonagon
Decagon
Q3: Give a few real-life examples of 3D shapes.
Answer:
Cube – Sugar cube, Rubik’s cube
Cuboid- A wooden rectangular box, matchbox
Cone- Icecream cone, Pyramid
Sphere- Football, Basketball
Cylinder- Gas cylinder, Cylindrical jar
Q4: What are basic solid shapes?
Answer:
The basic solid shapes are Cube, Cuboid, Cone, Sphere, Hemisphere and Cylinder.
Last Updated :
17 May, 2023
Like Article
Save Article
Как рисовать геометрические фигуры на плоскости
Правильный рисунок геометрической фигуры к задаче по геометрии – почти половина решения задачи.
Да-да, настолько он важен!
При правильном построении он поможет тебе не запутаться в данных и увидеть новые детали!
И сейчас ты научишься изображать объемные геометрические фигуры на плоскости. Это очень важно в стереометрии.
Поехали!
Как нарисовать пространственную фигуру так, чтобы было видно, что она объемная?
Есть несколько правил, применяя которые, ты всегда будешь получать красивые и понятные чертежи к своим задачам. Итак:
Как рисовать линии в трехмерном пространстве
Все линии (ребра, высоты, линии сечения), которые были бы не видны, если бы то, что мы рисуем, было бы сделано из глины (например) изображаются пунктиром. А все видные линии – сплошными.
Вот, смотри на несколько уже готовых чертежей, и поймешь, о чем речь.
Но возникает вопрос: а как вообще дойти до готового чертежа, где что-то должно быть сплошным, а что-то пунктиром?
Следующие правила как раз об этом.
Как рисовать квадраты и прямоугольники объемными
Все квадраты и прямоугольники, которые лежат в горизонтальной плоскости, нужно изображать параллелограммами, а прямоугольные треугольники – с острым углом, вместо прямого.
Видишь, похоже, будто треугольники прямоугольник лежат в плоскости.
Круги на плоскости
Все круги превращаются в овалы (тоже в горизонтальной плоскости)
Пирамида на плоскости
Когда рисуешь треугольную пирамиду, нужно сперва нарисовать «косой» четырехугольник:
А потом добавить еще два ребра:
И никогда ничего не сольется! Можно смело проводить высоту и строить сечения:
С четырехугольной пирамидой сложнее, но тоже разумно сперва прорисовать контур, а потом добавлять ребра.
Но только в исходном четырехугольнике одна из сторон должна быть параллельна взгляду:
А потом проводим параллельные:
И осталось только соединить:
Получилась красивая пирамида – Хеопс тоже не отказался бы 🙂
И осталось самое сложное – шестиугольная пирамида.
Чаще всего нужна правильная. Здесь уже сперва основание! Но…как мне нарисовать правильный шестиугольник, чтобы было похоже, что он лежит? Его нужно нарисовать приплюснутым (но соблюдая все параллельности: \( \left( AB||ED;\ \ BC||FE;\ \ AF||CD;\ \ BE||CD \right)\)
Потом из центра основания провести перпендикуляр, чтобы легче найти вершину.
И потом уже соединить вершину с вершинами основания.
И не думай, что шестиугольная пирамида получится с первого раза – нужно тренироваться!
Параллелепипед на плоскости
Тут сперва нужно нарисовать основание в виде параллелограмма:
Потом одну боковую грань:
А потом все остальные – и главное – соблюдать параллельность.
Призма на плоскости
Если нужно изобразить треугольную призму, то рисовать нужно так, чтобы угол треугольника смотрел на нас – живее получится. Вот:
А затем боковые ребра:
И потом верхнее основание:
Шар на плоскости
Сначала рисуем круг:
А потомобавим две дуги, чтобы получился такой овал с острыми краями. И ставим центр.
Цилиндр на плоскости
Рисуем овал и отмечаем его центр:
Проводим две образующие:
И «закрываем» верхним основанием. Обрати внимание на то, как расположены центры верхнего и нижнего овалов.
Рисуем на плоскости конус
Рисуем овал:
И делаем угол:
Обрати внимание: образующие (стороны угла) касаются основания, поэтому центр основания и две точки на нём не лежат на одной прямой (в отличие цилиндра).
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».
Основные понятия
Основные геометрические фигуры на плоскости — это точка и прямая линия. А простейшие фигуры — это луч, отрезок и ломаная линия.
Минимальный объект в геометрии — точка. Ее особенность в том, что она не имеет размеров: у нее нет высоты, длины, радиуса. У точки можно определить только ее расположение, которое принято обозначать одной заглавной буквой латинского алфавита.
Из множества точек может получится линия, а из нескольких соединенных между собой линий — геометрические фигуры.
Обучение на курсах по математике поможет быстрее разобраться в видах и свойствах геометрических фигур.
Каждая математическая фигура имеет собственную величину, которую можно измерить при помощи формул и внимательности.
Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.
Периметром принято называть сумму длин всех сторон многоугольника. Периметр обозначается заглавной латинской P.
Если параметры переданы в разных единицах измерения длины, нужно перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
- квадратный миллиметр (мм2);
- квадратный сантиметр (см2);
- квадратный дециметр (дм2);
- квадратный метр (м2);
- квадратный километр (км2);
- гектар (га).
Геометрические тела — часть пространства, которая ограничена замкнутой поверхностью своей наружной границы.
Если все точки фигуры принадлежат одной плоскости, значит она является плоской.
Объемная фигура — геометрическая фигура, у которой все точки не находятся на одной плоскости.
Примеры объемных геометрических фигур:
- шар,
- конус,
- параллелепипед,
- цилиндр,
- пирамида,
- сфера.
Рассмотрим подробнее некоторые фигуры, разберем их определения и свойства.
Домашний лицей для 5–11 классов
Занятия где и когда удобно, 10+ кружков на выбор, никакого стресса с домашками и нудных родительских собраний
Прямоугольник
Прямоугольник — параллелограмм, у которого все углы прямые.
Свойства прямоугольника:
- Диагонали прямоугольника равны и делятся в точке пересечения пополам.
- Около прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали.
Узнать площадь прямоугольника помогут следующие формулы:
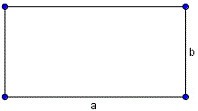
- S = a × b, где a, b — ширина и высота прямоугольника.
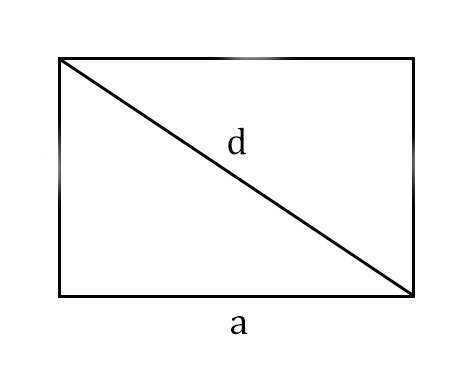
- S = a × √(d2 — а2), где а — известная сторона, d — диагональ.
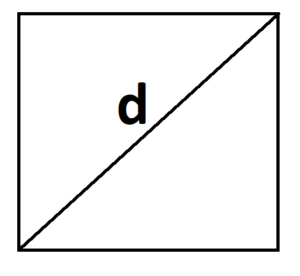
Диагональ — это отрезок, который соединяет противоположные вершины фигуры. Он есть во всех фигурах, число вершин которых больше трех.
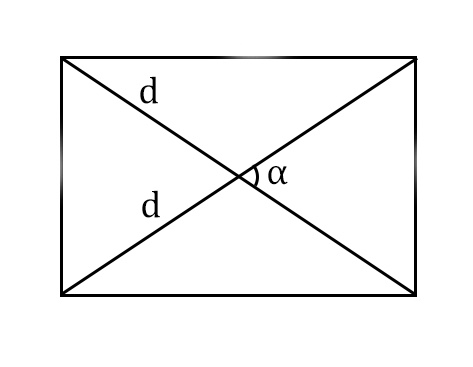
- S = 0,5 × d2 × 𝑠𝑖𝑛(𝑎), где d — диагональ.
Периметр прямоугольника — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
Выберите идеального репетитора по математике
15 000+ проверенных преподавателей со средним рейтингом 4,8. Учтём ваш график и цель обучения
Квадрат
Квадрат — это тот же прямоугольник, у которого все стороны равны.
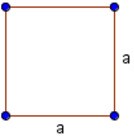
Свойства квадрата:
- Все стороны равны.
- Все углы равны и составляют 90 градусов.
- Диагонали квадрата равны и перпендикулярны.
- У квадрата центры вписанной и описанной окружности совпадают и находятся в точке пересечения его диагоналей.
Найти площадь квадрата легко:
- S = а2, где a — сторона квадрата.
- S = d2 : 2, где d — диагональ.
Периметр квадрата — это длина стороны, умноженная на четыре.
P = 4 × a, где a — длина стороны.
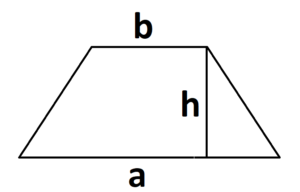
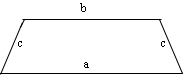
Трапеция
Трапеция — это четырехугольник, у которого две стороны параллельны, а две не параллельны.
Основное свойство: в трапецию можно вписать окружность, если сумма ее оснований равна сумме боковых сторон.
Как найти площадь трапеции:
S = (a + b) : 2 × h, где a, b — два разных основания, h — высота трапеции.
Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны и был расположен перпендикулярно к этим основаниям.
Формула периметра для равнобедренной трапеции отличается от прямоугольника тем, что у равнобедренной трапеции есть две равные стороны.
P = a + b + 2 × c, где a, b — параллельные стороны, c — две длины одинаковых сторон.
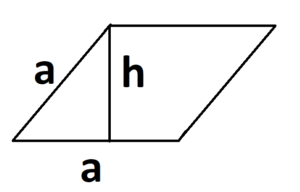
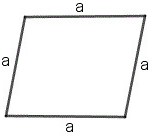
Параллелограмм и ромб
Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны
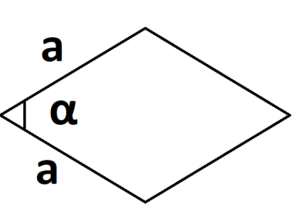
Ромб — это параллелограмм с равными сторонами.
Свойства параллелограмма:
- Противоположные стороны и углы равны.
- Сумма любых двух соседних углов равна 180 градусам.
- Диагонали пересекаются и точкой пересечения делятся пополам.
- Каждая диагональ делит фигуру на два равных треугольника.
Общие формулы расчета площади фигур:
- S = a × h, где a — сторона, h — высота.
- S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними. В случае с ромбом стороны равны, поэтому формула примет вид S = a × a × sinα или S = a2 × sinα.
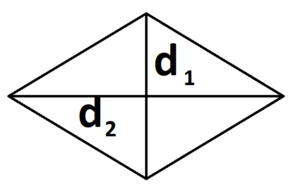
- Для ромба: S = 0,5 × (d1 × d2), где d1,d2 — две диагонали. Для параллелограмма: S = 0,5 × (d1 × d2) × sinβ, где β — угол между диагоналями.
Периметр ромба — это произведение длины стороны на четыре.
P = 4 × a, где a — длина стороны.
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
Треугольник
Треугольник — это такая фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки принято называть вершинами, а отрезки — сторонами.
Виды треугольников:
- Прямоугольный. Один угол прямой, два других менее 90 градусов.
- Остроугольный. Градус угла больше 0, но меньше 90 градусов.
- Тупоугольный. Один угол тупой, два других острые.
Свойства треугольника:
- В треугольнике против большего угла лежит большая сторона — и наоборот.
- Сумма углов треугольника равна 180 градусов.
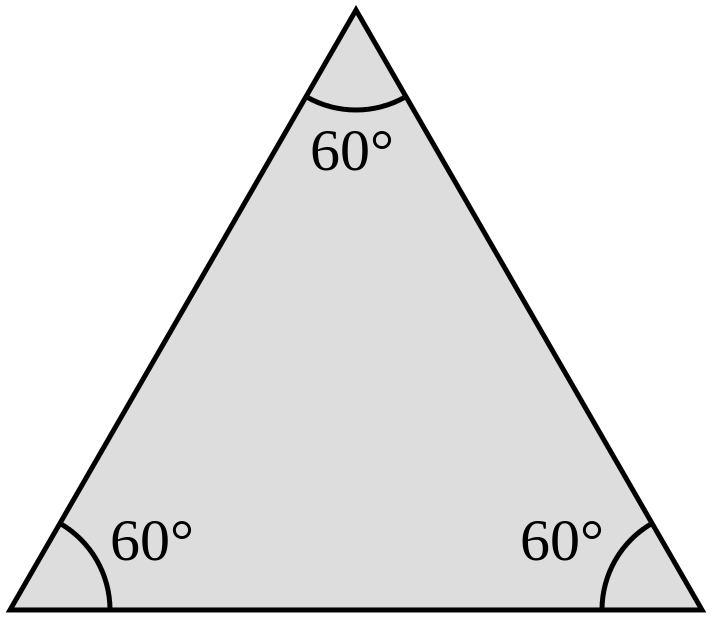
- Все углы равностороннего треугольника равны 60 градусам.
- В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Рассчитать площадь треугольника можно несколькими способами по исходным данным, давайте их рассмотрим.
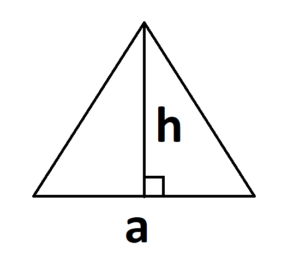
- Если известна сторона и высота.
S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.
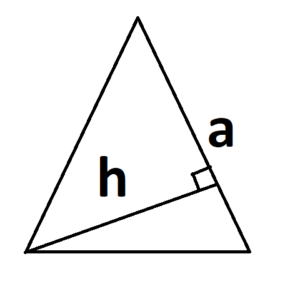
Основание может быть расположено иначе, например так:
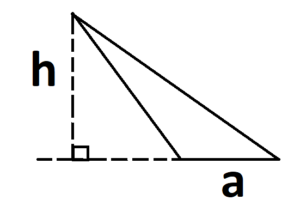
При тупом угле высоту можно отразить на продолжение основания:
При прямом угле основанием и высотой будут его катеты:
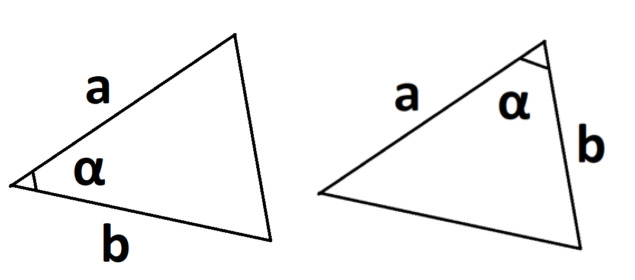
- Если известны две стороны и синус угла.
S = 0,5 × a × b × sinα, где a и b — две стороны, sinα — синус угла между ними.
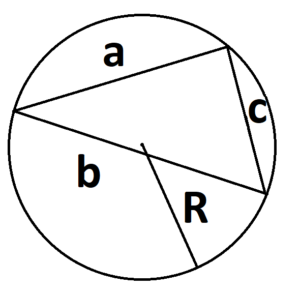
- Если есть радиус описанной окружности.
S = (a × b × с) : 4 × R, где a, b и с — стороны треугольника, а R — радиус описанной окружности.
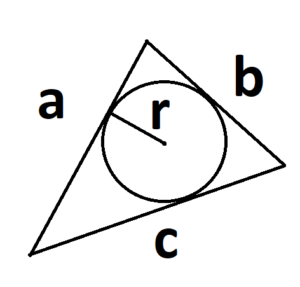
- Если есть радиус вписанной окружности.
S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.
Периметр треугольника — это сумма длин трех его сторон.
P = a + b + c, где a, b, c — длина стороны.
Формула измерения периметра для равностороннего треугольника — это длины стороны, умноженная на три.
P = 3 × a, где a — длина стороны.
Круг
Круг — это это часть плоскости, которая лежит внутри окружности.
Окружность — это граница круга.
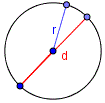
Радиус окружности — это расстояние от центра окружности до любой точки на ней.
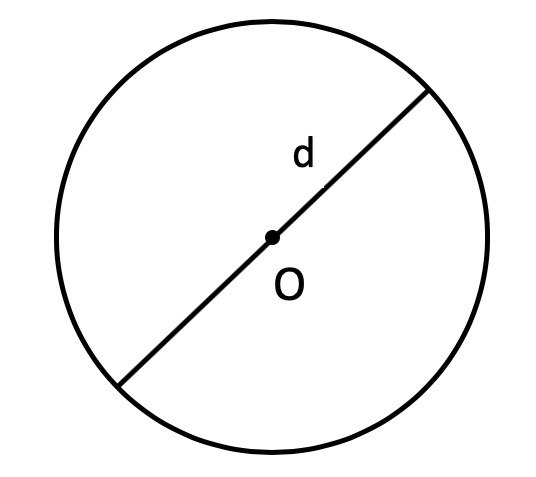
Диаметр круга — это отрезок, который соединяет две точки на окружности и проходящий через ее центр. Диаметр круга равен двум его радиусам.
Формулы площади круга:
- S = π × r2, где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
- S = π × d2 : 4, где d — это диаметр.
- S = L2 : (4 × π), где L — это длина окружности.
Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.
L = d × π = 2 × r × π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Простейшие геометрические фигуры карандашом – начальная стадия рисования любого объекта. Об этом свидетельствует компьютерное моделирование. Как и компьютерные трехмерные объекты включают в себя множество фигур, изображение делится на формы.
Особенности построения геометрических фигур
Рисунок геометрических фигур карандашом имеет такие этапы:
| № | Этап | Описание |
| 1 | Анализ модели | Необходимо представить фигуру как каркас из точек и линий. Прорисовывание невидимых линий – главный методологический прием, помогающий рисовать сложные модели. |
| 2 | Наметка линий и вершин | Для этого нужно совершать легкие скользящие движения карандашом, не надавливая на него слишком сильно. |
| 3 | Обозначение видимых ребер | Следует детально прорисовать линии, которые видимы зрителю. Например, если изображается шар или конус, то детально прорисовываются края формы. |
| 4 | Штриховка | С ее помощью можно отобразить расположение теней. |
Штриховка
Штриховка – важный элемент в изображении трехмерных объектов. С ее помощью художник передает тень.
Правила, которые следует запомнить начинающему творцу, следующие:
- Штриховка выполняется только по форме предмета. Иногда можно совмещать штриховки, что способствует усилению тени.
- Заполнение штрихом следует начинать с теневых областей. Если это куб, то штрихами должна быть заполнена 1 из его граней, а границей светотени станут ребра куба. В случае с шаром, цилиндром и конусом границы не четкие, а более размытые.
- Предпочтение лучше отдавать вертикальной штриховке. Начинать следует от ближней части и затем следовать дальше – вглубь рисунка, при этом уменьшая нажим карандашом. От этого штрих светлеет и становится заметно, как поверхность постепенно уходит вдаль.
- Освещенную область нужно начинать штриховать от себя.
Свет и тень
Любая тень образуется, если имеется источник света. Художник должен заранее определить, где именно располагается этот источник и с какой стороны падают на предмет лучи. Если при рисовании возникают трудности со светотенью, следует потренироваться на простом варианте.
Применять можно одну из 2-х техник – штриховку или растушевку. Перед работой рекомендуется включить свет, который будет направлен на предмет. Также важно, чтобы в помещении не было других, более ярких источников света.
Начинающий художник должен запомнить, что существуют следующие участки на рисунке:
| Участок | Описание |
| Блик | Часть рисунка, отражающая свет лампы или солнечного луча. |
| Свет | Области, освещенные лучами под прямым углом. |
| Полутень | Области, располагающиеся между светом и тенью. Их еще называют промежуточными. |
| Тень | Это не освещенные области. |
| Рефлекс | Это освещаемый участок, который получается от предметов поблизости. Огромную роль играет яркость падающего света: чем он ярче, тем более насыщенной будет тень. |
| Падающая тень | Тень от фигуры на то, что находится вокруг. Например, на горизонтальную поверхность, где располагается фигура или стена возле нее. |
Важно уметь находить границу между светом и тенью. Ее форма зависима от рисуемого изображения. К примеру, на шаре эта граница одна, а на кубе – другая. Проблема поиска границы заключена в том, что она обычно размытая. Изредка она бывает четкой: чем ярче свет, тем четче граница.
Например:
- если посмотреть на шар, находящийся под яркими прямыми лучами, можно заметить, что граница светотени имеет изгиб и похожа на овал;
- в случае с цилиндром граница превратится в прямую линию;
- на кубе эта граница проходит прямо по ребру.
В изобразительном искусстве применяется прием, носящий название – «кьяроскуро». Он основан на противопоставлении освещенной и затененной областей. При искусственном освещении образуется среда, где свет становится слишком ярким, а тень – очень темной, что придает насыщенности и резкости.
Рисование в перспективе: куб
Рисунок геометрических фигур карандашом следует начинать с куба.
Обычно применяется белая гипсовая модель, на которой отчетливо видна светотень. Модель лучше приобрести или сделать самостоятельно, фотографию использовать не рекомендуется.
Для изображения необходимо:
- Наметить местоположение фигуры. Разместить ее немного выше центра листа, при этом она должна быть подвинута в сторону теневой области. Это способствует равновесию композиции.
- Провести первую вертикальную линию. Это будет ближайшее к зрителю ребро куба. Засечками нужно ограничить высоту куба.
- Изобразить основание фигуры. Начинать необходимо с видимых линий, точно определив углы их наклона.
- Нарисовать линии, располагающиеся вверху. Перед этим необходимо вспомнить принципы линейной перспективы. Один из них гласит: видимый размер фигур при удалении становится меньше. Линия горизонта располагается на уровне глаз, однако при изменении положения головы эта линия может подняться или опуститься.
- Определить, как сократились боковые грани фигуры.
- Нарисовать дальние линии, не забывая про линии, которые не видны.
- После выполнения и проверки построения выделить ближайшие линии. Чем они ближе, тем более темными их следует сделать.
- Выполнить штриховку. Сначала заполнить штрихом теневые области, а затем перейти к освещенной поверхности. Ближний угол следует оставлять незаштрихованным, а дальнюю часть заполнить легким штрихом.
- Подчеркнуть объем формы, сделав тональные акценты.
Рисование геометрических тел вращения
Геометрические тела вращения начинают рисовать только после освоения изображения куба. Изначально фигуры изображают по отдельности, после – пробуют натюрморт.
Для успеха прорисовывания сложных форм, начинают с изображения простых. Модели можно приобрести в магазине или изготовить своими силами. Для этого используется картон или толстая бумага.
Фигуры нельзя заменять их фотографиями: срисовывание объемных фигур с плоской поверхности лишено смысла и не несет пользы.
Конус
Слово «конус» имеет греческое происхождение. Оно переводится как «сосновая шишка». Такое название фигуре дали потому, что она похожа на шишку или на колпак.
Если же выражаться математическим языком, эта фигура является симметричным телом, которое образуется вследствие объединения лучей, берущих начало из 1-й точки (вершины конуса) и проходящих через плоскую поверхность.
Основанием является круг. Если установить модель конуса основанием на горизонтальную поверхность и посмотреть на нее сбоку, она предстанет перед глазами как треугольник.
Однако в зависимости от угла, под которым смотрят на фигуру, нижняя ее часть, может превращаться в полукруг, поэтому при изображении конуса следует учитывать угол зрения. Также важно, с которой стороны на фигуру падает свет для последующего наложения штриховки.
Рисовать карандашом объемную геометрическую фигуру конуса следует следующим образом:
- Наметить место и размеры фигуры, которая не должна быть очень маленькой или, наоборот, большой. Конус располагается выше середины листа: его верхняя часть оптически более легкая, за счет большего свободного пространства.
- Наметить верхнюю часть фигуры и провести горизонтальную линию. Она будет исполнять роль оси основания.
- Обозначить ширину основания засечками.
- Провести вертикаль по центру фигуры.
- Соединить вершины с основанием.
- Визуально сделать крайние линии удаленными от зрителя, сделав их светлее.
- Строить эллипс: для передачи объема ближняя часть овала должна быть более темной.
- Продолжить работу над объемом. Для этого найти границу тени и света в вершине фигуры и проходящую к основанию. Верхняя часть линии должна быть четкой, а ее отдаленный край – более светлым.
- Осуществить штриховку, двигаясь по вертикали от вершины и доводя до основания. Чтобы лучше передать форму, ввести штрихование и по горизонтали.
- Обозначить контраст света и тени, сделав верхнюю часть более светлой. От горизонтальной поверхности, на которой установлена фигура, подсветить теневую часть.
Цилиндр
Цилиндр имеет 2 основания – внизу и вверху. Оба они имеют форму круга и абсолютно равны по размеру. Образующая цилиндра – вертикаль, расположенная перпендикулярно основанию.
Рисунок геометрических фигур карандашом в форме цилиндра выполняется в следующем порядке:
- На листе обозначить местоположение объекта и легкой штриховкой выявить объем формы. Не нужно слишком надавливать на карандаш, особенно когда рисуются вспомогательные линии. Применение ластика лучше сводить к минимуму.
- Определить высоту и ширину фигуры.
- Провести ось. Она должна делить фигуру пополам.
- Проконтролировать, чтобы верхний эллипс был чуть меньше. При взгляде на модель легко заметить, что верхнее основание развернуто меньше.
- Перейти к работе со светотенью. Граница ее прорисовывается по вертикали от одного основания к другому. Учитывая плавность изменения формы, сделать границу размытой. Штрих следует вертикально. Области, которые удаляются, на свету темнеют, а в тени становятся светлыми. Верхний эллипс попадает в область полутени, если источник света находится сбоку.
- Уточнить форму. Для этого используется штриховка в горизонтальном направлении. Поскольку верхняя часть приближена к свету, она должна быть немного светлее.
Шар
Шар считается простейшей фигурой, недаром такую форму под воздействием сил природы приобретают все планеты и звезды. Однако изобразить шар – задача не из простых.
Первые трудности могут возникнуть с рисованием окружности, затем приходится сталкиваться с серьезными проблемами, появляющимися при штриховке.
Перед работой модель шара рекомендуется осветить мягким светом. В этом случае не будет резких теней, что значительно упростит задачу.
Последовательность рисования шара следующая:
- Изобразить окружность, которая станет основой фигуры. В центре бумаги провести прямую, а в центре этой прямой поставить точку. Через нее провести еще 1 прямую, перпендикулярную 1-й. При проведении этих линий не нужно сильно давить на карандаш.
Крайние точки линий нужно соединить так, чтобы образовалась окружность. - Наложить тени. Нужно определить, откуда попадает свет, и поставить точку в самой освещенной части. Ширину тени необходимо отметить штриховкой.
- Провести диаметр через центр фигуры перпендикулярно лучам света.
- На основании диаметра изобразить эллипс. Он обозначает границы светотени.
- Поверхность фигуры условно разделить на несколько областей в зависимости от степени освещенности. Самая светлая область – это блик, ее можно оставить не закрашенной. Вокруг нее – светлое пятно, а далее постепенно переходить к тени. Изображать тень нужно дугообразными штрихами.




Для рисования натюрмортов из геометрических фигур необходимо:
- Подготовить 3-4 фигуры с разными характеристиками. Например, это может быть куб, шар и цилиндр.
- Расставить фигуры и подготовить драпировку ткани, на которой они стоят.
- Выставить спокойное, рассеянное освещение.
- Выбрать ракурс для срисовывания. Лучше, если он будет фронтальным.
- Определиться с расположением рисунка и приступить к работе.
Для начинающего художника рисование геометрических фигур карандашом подобно обучению алфавита для тех, кто изучает язык. Такая тренировка поможет в дальнейшем при создании сложных фигур и композиций на бумаге.
Видео о рисовании геометрических фигур
Рисунок геометрических фигур карандашом:










.webp)